Academic CV

• Click here for full Academic CV
• Click here for list of publications
• Click here for list of talks

---

Research Area I - Benford's Law

A century-old empirical observation now called Benford's Law says that the significant digits of many real datasets are logarithmically distributed, rather than uniformly distributed, as might be expected. This research includes discoveries that help explain the ubiquity of Benford data sets. For example, it has now been shown that iterations of many common functions (including all polynomials, power, exponential, and trigonometric functions, as well as compositions thereof), dynamical systems and differential equations, geometric Brownian motion (hence most stock market models), mixtures of data from different sources, and Newton's method, all produce Benford sequences. These publications also include applications to fraud detection and to diagnostic tests for mathematical models, many examples, and open Benford-related problems in dynamical systems, probability, number theory, and differential equations.

In Episode 4 ("Digits") of the new Netflix series Connected: The Hidden Science of Everything, Latif Nasser interviewed Ted on the topic of Benford's Law (streaming globally August 2, 2020).

The mathematics of Benford's law: a primer (with A. Berger), Statistical Methods & Applications (2020) [PDF].

An Introduction to Benford's Law (in collaboration with A. Berger). Princeton University Press, 2015.
For Amazon link, click here.

For American Scientist article on this topic, click here.

For a free searchable online bibliographic database on Benford's Law, see the Benford Online Bibliography, www.benfordonline.net.

---

Research Area II - Optimal Stopping Theory

In many basic processes in science (and in life), there is an element of chance involved, and a crucial problem is deciding when to stop. The process could be debugging large software programs, proofreading a paper, waiting to buy Google stocks, performing medical experiments, looking at houses to buy, gathering laboratory data, or interviewing for a new secretary (or spouse). The typical framework is that a sequence of random variables is being observed, and the objective is to decide when to stop in order to maximize the expected reward. These publications include basic "prophet inequalities" (comparisons of the expected return of a gambler who has foresight, or inside information, with a gambler who does not' game-theoretic extensions to the classical secretary problem, and determiation of optimal rules and optimal bounds for generalized stopping.

For American Scientist article on this topic, click here. For the French version in Pour la Science, click here.

---

Research Area III - Fair Division Problems

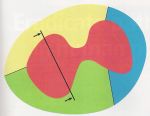The general subject of this research is the question of whether an object (such as a cake or piece of land) can be divided among a number of people so that each receives a portion he considers a fair share, according to his own values. (Formally, there are n measures on the same object - a measurable space - and a typical goal is to find a partition of the object into n pieces so that the minimum value of the i-th measure on the i-th piece is as large as possible). These publications include generalizations of Steinhaus'classical "Ham Sandwich Problem", Neyman and Pearson's "Bisection Problem", and Fisher's "Problem of the Nile", determination of optimal bounds and extreme-case measures, generalizations of Lyapounov's Convexity Theorem, and applications to disarmament, dividing inheritances, and lotterized allocations of indivisible goods.

For 2018 American Scientist article on "Slicing Sandwiches, States, and Solar Systems", click here.

For 2008 American Scientist article on "Mathematical Devices for Getting a Fair Share", click here.

---

Research Area IV - Scientific Miscellany

Part of Ted's recreational scientific research includes raising unorthodox questions in various fields, and this has led to new collaborations, a "Weird Science" award, and a good bit of controversy.

---

Letters to the Editor

• Benford's Law Blunders, Letter to the Editor, The American Statistician 65(2):141, 2011.
• Hoisting the Black Flag, Letter to the Editor, Notices of the AMS, January 2010.
• Response to Letters to the Editor, American Scientist Online - "Gleaning the Cube", July-August 2007.
• Response to Letters to the Editor, American Scientist Online - "Your Number's Up", May-June 2007. (Online link is incorrect.)
• Review of The Golden Ratio, Letter to the Editor, Notices of the AMS, Vol. 52, no. 6, 2005.
• Response to "Benfords Gesetz", Brief an die Herausgeber, Deutsche Mathematische Verein, Mitteilungen 3/2001, p. 4.

---

Scientific Collaborators

• Jon Aaronson, University of Tel Aviv, Israel
• Rosalind Arden, London School of Economics
• Arno Berger, University of Alberta, Canada
• Lisa Bloomer, Middle Tennessee State University
• Frans Boshuizen, Vrije U. Amsterdam; SNS REALL, Netherlands
• Leonid Bunimovich, Georgia Institute of Technology
• Robert Burton, University of Oregon
• Albert C. Censullo, California Polytechnic State U., San Luis Obispo
• Marco Dall’Aglio, LUISS Guido Carli University, Italy
• Herold Dehling, Ruhr-Universität Bochum, Germany
• Stephen Demko, Georgia Institute of Technology
• John Elton, Georgia Institute of Technology
• Robert Foley, Georgia Institute of Technology
• Ronald Fox, Georgia Institute of Technology
• Jeffrey Geronimo, Georgia Institute of Technology
• David Gilat, University of Tel Aviv, Israel
• Arie Hordijk, Leiden University, Netherlands
• Bahar Kaynar, Vrije Universiteit Amsterdam, Netherlands
• Douglas Kennedy, Cambridge University, U.K.
• Robert Kertz, Georgia Institute of Technology
• Viacheslav V. Khruschov, Kurchatov Institute Moscow
• Ulrich Krengel, University of Göttingen, Germany
• James Mann, RenaissanceRe Syndicate Management
• Jack Miller, Lawrence Berkeley National Laboratory
• Michael Monticino, University of North Texas
• Kent Morrison, California Polytechnic State U., San Luis Obispo
• Victor Perez-Abreu, Centro de Investigación en Matemáticas, Mexico
• Victor Pestien, University of Miami
• Ad Ridder, Vrije Universiteit Amsterdam, Netherlands
• Erika Rogers, California Polytechnic State U., San Luis Obispo
• Klaus Schuerger, University of Bonn, Germany
• David Sitton, Planning Systems Inc.
• Carl Spruill, Georgia Institute of Technology
• Sergei Tabachnikov, Penn State University
• Yung Tong, Georgia Institute of Technology
• Jan Van der Wal, University of Amsterdam, Netherlands
• Benjamin Weiss, Hebrew University, Israel

---